 Στο κεφάλαιο αυτό θα εξετάσουμε την βασική ιδιότητα των κλασμάτων που είναι η ισοδυναμία. Θα την εξετάσουμε όμως όπως εμφανίζεται στα πραγματικά φαινόμενα και σε καμία περίπτωση δε θα προχωρήσουμε ούτε θα δούμε την ισοδυναμία μέσα από μαθηματικές ιδιότητες, όπως πολλαπλασιασμός και διαίρεση αριθμητή και παρανομαστή κτλ.
Στο κεφάλαιο αυτό θα εξετάσουμε την βασική ιδιότητα των κλασμάτων που είναι η ισοδυναμία. Θα την εξετάσουμε όμως όπως εμφανίζεται στα πραγματικά φαινόμενα και σε καμία περίπτωση δε θα προχωρήσουμε ούτε θα δούμε την ισοδυναμία μέσα από μαθηματικές ιδιότητες, όπως πολλαπλασιασμός και διαίρεση αριθμητή και παρανομαστή κτλ.
Θα δείξουμε την ισοδυναμία των κλασμάτων μέσα από πραγματικές καταστάσεις που είναι οικείες στους μαθητές όπως ο χωρισμός συνεχών μεγεθών (πχ. πίτσα, σοκολάτα) και διακριτών μεγεθών (π.χ. τα νομίσματα). Έτσι αν έχουμε τρεις πίτσες όπου η πρώτη είναι κομμένη στα δύο, η δεύτερη στα τέσσερα και η τρίτη στα οχτώ, το μισό σε κάθε πίτσα θα φαίνεται με διαφορετικό τρόπο. Στην πρώτη θα είναι το 1/2, στη δεύτερη τα 2/4 και στην τρίτη τα 4/8. Σε διακριτές καταστάσεις όπως για παράδειγμα στα μπισκότα, η ισοδυναμία των κλασμάτων εμφανίζεται με έναν τρόπο πιο δύσκολο για τα παιδιά.Μπορούμε να δούμε τα 3 μπισκότα ως ένα από τα τέσσερα μέρη στα οποία χωρίσαμε τα 12 μπισκότα, δηλαδή το 1/4. Αλλά μπορούμε να δούμε το ένα μπισκότο ως το 1/12 όλων των μπισκότων – άρα τα 3 μπισκότα ως τα 3/12 του όλου. Άρα κάποιες ποσότητες μπορούμε να τις αποδίδουμε σε δύο κλάσματα, όπως για παράδειγμα το 1/4 και τα 3/12. Τα κλάσματα αυτά τα ονομάζουμε ισοδύναμα.
πηγή:Μαθηματικά Γ τάξης, βιβλίο δασκάλου
ΦΥΛΛΑ ΕΡΓΑΣΙΑΣ
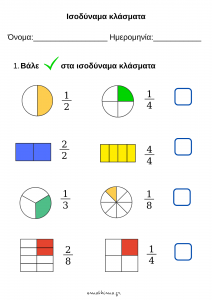
Φύλλο εργασίας _Ισοδύναμα κλάσματα (1)
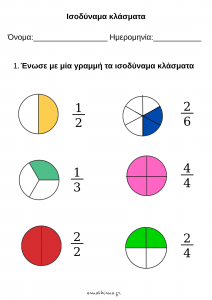
Φύλλο εργασίας _Ισοδύναμα κλάσματα (2)
Φύλλο εργασίας 4
Υλικό κυκλοφοριακής αγωγής
Φύλλο εργασίας 5
ΔΙΑΔΡΑΣΤΙΚΕΣ ΕΦΑΡΜΟΓΕΣ
πηγή: Bbbb12


Στο βιβλίο μου εδώ και 9 χρόνια έχω το θεώρημά μου των μεγάλων αριθμών το οποίο αναβαθμίζει τα ισοδύναμα κλάσματα .
π.χ. Αριθμητής = 17 Το πηλίκο της διαίρεσης είναι 8,5
Παρονομαστής = 2
Το θεώρημά μου μου λέει να κολλάω αριθμητή με αριθμητή και παρονομαστή με παρονομαστή και να κολλάω και το ψηφίο μηδέν όπου μου χρειάζεται .
Αριθμητής = 17171717171717171717171717171717
Παρονομαστής = 2020202020202020202020202020202
Αν διαιρέσετε θα βρείτε το ίδιο πηλίκο 8,5
Μπορώ να συνεχίσω να κολλάω και πέρα από το Σύμπαν .
Αυτό και δεκάδες άλλες ανακαλύψεις μου το Υπουργείο της Παιδείας δεν θέλει να γράψει στα βιβλία των Μαθηματικών . Συνδικαλιστές αγράμματοι είναι τι περιμένετε αυτοί έχουν ξεχάσει και την προπαίδεια . διότι αν την ήξεραν δεν θα την έγραφαν με αντιμεταθετική ιδιότητα .
Στα τελευταία χρόνια Έλληνες και ξένοι Μαθηματικοί έχουν πάρει βραβεία και βραβεία και Νόμπελ στα Μαθηματικά και δεν μπόρεσαν να βρουν το θεώρημά μου αυτό Τις διαστάσεις των ευθυγράμμων σχημάτων και στερεών τις μεγαλώνει όσο θέλουμε .
έχεται κάνει μια απλή πλατφόρμα που δεν καταλαβαινουν τα παιδια και εγω είμαι ένα παιδι που δεν καταλαβαίνω τιποτα από ότι λετε
Το υλικό της σελίδας σε καμία περίπτωση δεν αντικαθιστά τον δάσκαλο και τη διδασκαλία. Είναι ενισχυτικό πάνω στην ύλη που έχετε διδαχθεί. Για οποιαδήποτε απορία πρέπει πάντα να ρωτάτε τον δάσκαλό σας.
ευχαριστώ πολύ 🙂
Το υλικό σας είναι εκπληκτικό! Στα μεγάλα πλεονεκτήματα της σελίδας σας είναι η πολύ καλή οργάνωση των φύλλων εργασίας ανά μάθημα, ανα κεφάλαιο κοκ. Αλλά και οι σύνδεσμοι που προσεγγίζουν ολικά ένα διδακτικό αντικείμενο πχ. Κλάσματα.
Σας ευχαριστούμε!
Γεια σας! Ο μικρος μου αδερφος παει 3η δημοτικου και εχει μια ασκηση με ισοδυναμα κλασματα ομως δεν την καταλαβαινει.Του την εχω εξηγησει παρα πολλες φορες αλλα αυτος τιποτα. Μηπως θα μπορουσατε να το εξηγηγησετε πιο απλα???